Hello Again Professor Hyde,We are currently working on ways to publish this text in a form other than HTML (e.g., Postscript, PDF, Frameviewer, hard copy, etc.). This, however, is a low-priority project. Please do not contact Randall Hyde concerning this effort. When something happens, an announcement will appear on "Randall Hyde's Assembly Language Page." Please visit this WEB site at http://webster.ucr.edu for the latest scoop.
Dallas gave me permission to take orders for the Computer Science 13 Manuals. We would need to take charge card orders. The only cards we take are: Master Card, Visa, and Discover. They would need to send the name, numbers, expiration date, type of card, and authorization to charge $95.00 for the manual and shipping, also we should have their phone number in case the company has any trouble delivery. They can use my e-mail address for the orders and I will process them as soon as possible. I would assume that two weeks would be sufficient for printing, packages and delivery time.
I am open to suggestions if you can think of any to make this as easy as possible.
Thank You for your business,
Kathy Chapman, Assistant
Printing and Reprographics
University of California
Riverside
(909) 787-4443/4444
x:=x+1, x is an integer. On any modern
computer this statement follows the normal rules of algebra as long as overflow
does not occur. That is, this statement is valid only for certain values
of x (minint <= x < maxint). Most programmers do not have a problem
with this because they are well aware of the fact that integers in a program
do not follow the standard algebraic rules (e.g., 5/2 <>
2.5).When adding and subtracting two numbers in scientific notation, you must
adjust the two values so that their exponents are the same. For example,
when adding 1.23e1 and 4.56e0, you must adjust the values so they have the
same exponent. One way to do this is to to convert 4.56e0 to 0.456e1 and
then add. This produces 1.686e1. Unfortunately, the result does not fit
into three significant digits, so we must either round or truncate the result
to three significant digits. Rounding generally produces the most accurate
result, so let's round the result to obtain 1.69e1. As you can see, the
lack of precision (the number of digits or bits we maintain in a computation)
affects the accuracy (the correctness of the computation).
In the previous example, we were able to round the result because we maintained
four significant digits during the calculation. If our floating point calculation
is limited to three significant digits during computation, we would have
had to truncate the last digit of the smaller number, obtaining 1.68e1 which
is even less correct. Extra digits available during a computation are known
as guard digits (or guard bits in the case of a binary format). They greatly
enhance accuracy during a long chain of computations.
The accuracy loss during a single computation usually isn't enough to worry
about unless you are greatly concerned about the accuracy of your computations.
However, if you compute a value which is the result of a sequence of floating
point operations, the error can accumulate and greatly affect the computation
itself. For example, suppose we were to add 1.23e3 with 1.00e0. Adjusting
the numbers so their exponents are the same before the addition produces
1.23e3 + 0.001e3. The sum of these two values, even after rounding, is 1.23e3.
This might seem perfectly reasonable to you; after all, we can only maintain
three significant digits, adding in a small value shouldn't affect the result
at all. However, suppose we were to add 1.00e0 1.23e3 ten times. The first
time we add 1.00e0 to 1.23e3 we get 1.23e3. Likewise, we get this same result
the second, third, fourth, ..., and tenth time we add 1.00e0 to 1.23e3.
On the other hand, had we added 1.00e0 to itself ten times, then added the
result (1.00e1) to 1.23e3, we would have gotten a different result, 1.24e3.
This is the most important thing to know about limited precision arithmetic:
The order of evaluation can effect the accuracy of the result.
You will get more accurate results if the relative magnitudes (that is,
the exponents) are close to one another. If you are performing a chain calculation
involving addition and subtraction, you should attempt to group the values
appropriately.
Another problem with addition and subtraction is that you can wind up with
false precision. Consider the computation 1.23e0 - 1.22 e0. This produces
0.01e0. Although this is mathematically equivalent to 1.00e-2, this latter
form suggests that the last two digits are exactly zero. Unfortunately,
we've only got a single significant digit at this time. Indeed, some FPUs
or floating point software packages might actually insert random digits
(or bits) into the L.O. positions. This brings up a second important rule
concerning limited precision arithmetic:
Multiplication and division do not suffer from the same problems as addition
and subtraction since you do not have to adjust the exponents before the
operation; all you need to do is add the exponents and multiply the mantissas
(or subtract the exponents and divide the mantissas). By themselves, multiplication
and division do not produce particularly poor results. However, they tend
to multiply any error which already exists in a value. For example, if you
multiply 1.23e0 by two, when you should be multiplying 1.24e0 by two, the
result is even less accurate. This brings up a third important rule when
working with limited precision arithmetic:
Often, by applying normal algebraic transformations, you can arrange a calculation
so the multiply and divide operations occur first. For example, suppose
you want to compute x*(y+z). Normally you would add y and z together and
multiply their sum by x. However, you will get a little more accuracy if
you transform x*(y+z) to get x*y+x*z and compute the result by performing
the multiplications first.
Multiplication and division are not without their own problems. When multiplying
two very large or very small numbers, it is quite possible for overflow
or underflow to occur. The same situation occurs when dividing a small number
by a large number or dividing a large number by a small number. This brings
up a fourth rule you should attempt to follow when multiplying or dividing
values:
Comparing floating pointer numbers is very dangerous. Given the inaccuracies
present in any computation (including converting an input string to a floating
point value), you should never compare two floating point values to see
if they are equal. In a binary floating point format, different computations
which produce the same (mathematical) result may differ in their least significant
bits. For example, adding 1.31e0+1.69e0 should produce 3.00e0. Likewise,
adding 2.50e0+1.50e0 should produce 3.00e0. However, were you to compare
(1.31e0+1.69e0) agains (2.50e0+1.50e0) you might find out that these sums
are not equal to one another. The test for equality succeeds if and only
if all bits (or digits) in the two operands are exactly the same. Since
this is not necessarily true after two different floating point computations
which should produce the same result, a straight test for equality may not
work.
The standard way to test for equality between floating point numbers is
to determine how much error (or tolerance) you will allow in a comparison
and check to see if one value is within this error range of the other. The
straight-forward way to do this is to use a test like the following:
if Value1 >= (Value2-error) and Value1 <= (Value2+error) then ...Another common way to handle this same comparison is to use a statement of the form:
if abs(Value1-Value2) <= error then ...Most texts, when discussing floating point comparisons, stop immediately after discussing the problem with floating point equality, assuming that other forms of comparison are perfectly okay with floating point numbers. This isn't true! If we are assuming that x=y if x is within y±error, then a simple bitwise comparison of x and y will claim that x<y if y is greater than x but less than y+error. However, in such a case x should really be treated as equal to y, not less than y. Therefore, we must always compare two floating point numbers using ranges, regardless of the actual comparison we want to perform. Trying to compare two floating point numbers directly can lead to an error. To compare two floating point numbers, x and y, against one another, you should use one of the following forms:
= if abs(x-y) <= error then ... <> (!=) if abs(x-y) > error then ... < if (x-y) < error then ... <= if (x-y) <= error then ... > if (x-y) > error then ... >= if (x-y) >= error then ...You must exercise care when choosing the value for error. This should be a value slightly greater than the largest amount of error which will creep into your computations. The exact value will depend upon the particular floating point format you use, but more on that a little later. The final rule we will state in this section is
1.mmmmmmm mmmmmmmm mmmmmmmmThe "mmmm..." characters represent the 23 bits of the mantissa. Keep in mind that we are working with binary numbers here. Therefore, each position to the right of the binary point represents a value (zero or one) times a successive negative power of two. The implied one bit is always multiplied by 20, which is one. This is why the mantissa is always greater than or equal to one. Even if the other mantissa bits are all zero, the implied one bit always gives us the value one[3]. Of course, even if we had an almost infinite number of one bits after the binary point, they still would not add up to two. This is why the mantissa can represent values in the range one to just under two.

With a 24 bit mantissa, you will get approximately 6-1/2 digits of precision
(one half digit of precision means that the first six digits can all be
in the range 0..9 but the seventh digit can only be in the range 0..x where
x<9 and is generally close to five). With an eight bit excess-128 exponent,
the dynamic range of single precision floating point numbers is approximately
2±128 or about 10±38.
Although single precision floating point numbers are perfectly suitable
for many applications, the dynamic range is somewhat small for many scientific
applications and the very limited precision is unsuitable for many financial,
scientific, and other applications. Furthermore, in long chains of computations,
the limited precision of the single precision format may introduce serious
error.
The double precision format helps overcome the problems of single preicision
floating point. Using twice the space, the double precision format has an
11-bit excess-1023 exponent and a 53 bit mantissa (with an implied H.O.
bit of one) plus a sign bit. This provides a dynamic range of about 10±308and
14-1/2 digits of precision, sufficient for most applications. Double precision
floating point values take the form shown below:
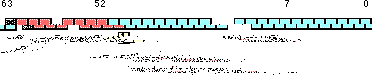
In order to help ensure accuracy during long chains of computations involving
double precision floating point numbers, Intel designed the extended precision
format. The extended precision format uses 80 bits. Twelve of the additional
16 bits are appended to the mantissa, four of the additional bits are appended
to the end of the exponent. Unlike the single and double precision values,
the extended precision format does not have an implied H.O. bit which is
always one. Therefore, the extended precision format provides a 64 bit mantissa,
a 15 bit excess-16383 exponent, and a one bit sign. The format for the extended
precision floating point value is shown below:

On the 80x87 FPUs and the 80486 CPU, all computations are done using
the extended precision form. Whenever you load a single or double precision
value, the FPU automatically converts it to an extended precision value.
Likewise, when you store a single or double precision value to memory, the
FPU automatically rounds the value down to the appropriate size before storing
it. By always working with the extended precision format, Intel guarantees
a large number of guard bits are present to ensure the accuracy of your
computations. Some texts erroneously claim that you should never use the
extended precision format in your own programs, because Intel only guarantees
accurate computations when using the single or double precision formats.
This is foolish. By performing all computations using 80 bits, Intel helps
ensure (but not guarantee) that you will get full 32 or 64 bit accuracy
in your computations. Since the 80x87 FPUs and 80486 CPU do not provide
a large number of guard bits in 80 bit computations, some error will inevitably
creep into the L.O. bits of an extended precision computation. However,
if your computation is correct to 64 bits, the 80 bit computation will always
provide at least 64 accurate bits. Most of the time you will get even more.
While you cannot assume that you get an accurate 80 bit computation, you
can usually do better than 64 when using the extended precision format.
To maintain maximum precision during computation, most computations use
normalized values. A normalized floating point value is one that has a H.O.
mantissa bit equal to one. Almost any non-normalized value can be normalized
by shifting the mantissa bits to the left and decrementing the exponent
by one until a one appears in the H.O. bit of the mantissa. Remember, the
exponent is a binary exponent. Each time you increment the exponent, you
multiply the floating point value by two. Likewise, whenever you decrement
the exponent, you divide the floating point value by two. By the same token,
shifting the mantissa to the left one bit position multiplies the floating
point value by two; likewise, shifting the mantissa to the right divides
the floating point value by two. Therefore, shifting the mantissa to the
left one position and decrementing the exponent does not change the value
of the floating point number at all.
Keeping floating point numbers normalized is beneficial because it maintains
the maximum number of bits of precision for a computation. If the H.O. bits
of the mantissa are all zero, the mantissa has that many fewer bits of precision
available for computation. Therefore, a floating point computation will
be more accurate if it involves only normalized values.
There are two important cases where a floating point number cannot be normalized.
The value 0.0 is a special case. Obviously it cannot be normalized because
the floating point representation for zero has no one bits in the mantissa.
This, however, is not a problem since we can exactly represent the value
zero with only a single bit.
The second case is when we have some H.O. bits in the mantissa which are
zero but the biased exponent is also zero (and we cannot decrement it to
normalize the mantissa). Rather than disallow certain small values, whose
H.O. mantissa bits and biased exponent are zero (the most negative exponent
possible), the IEEE standard allows special denormalized values to represent
these smaller values[4]. Although the use of denormalized
values allows IEEE floating point computations to produce better results
than if underflow occurred, keep in mind that denormalized values offer
less bits of precision and are inherently less accurate.
Since the 80x87 FPUs and 80486 CPU always convert single and double precision
values to extended precision, extended precision arithmetic is actually
faster than single or double precision. Therefore, the expected performance
benefit of using the smaller formats is not present on these chips. However,
when designing the Pentium/586 CPU, Intel redesigned the built-in floating
point unit to better compete with RISC chips. Most RISC chips support a
native 64 bit double precision format which is faster than Intel's extended
precision format. Therefore, Intel provided native 64 bit operations on
the Pentium to better compete against the RISC chips. Therefore, the double
precision format is the fastest on the Pentium and later chips.